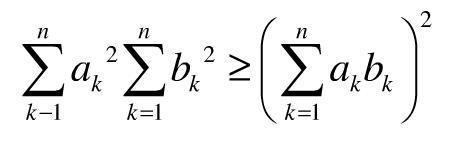最早的教材讲线性规划，这种题用圆和直线来做，后来教材学参数方程，这种题可以用三角代换来做，新教材讲不等式，所以就用柯西不等式来做。
柯西不等式证明！
柯西不等式(a^2＋b^2)(c^2 + d^2)≥(ac+bd)^2 等号成立条件：ad=bc证明(a^2+b^2)(c^2+d^2) （a,b,c,d∈R) ＝a^2·c^2 ＋b^2·d^2＋a^2·d^2＋b^2·c^2 ＝a^2·c^2 ＋2abcd＋b^2·d^2＋a^2·d^2－2abcd＋b^2·c^2 ＝(ac＋bd)^2＋(ad－bc)^2 ≥(ac＋bd)^2，等号在且仅在ad－bc=0即ad=bc时成立。根据你题目意思，a、b≥0，为正整数原式=（√a^2+√b^2）（1/√a^2+√n^2/√b^2）≥（1+√n）^2n=1时，原式有最小值4
柯西不等式的写法及证明
中学数学基本上是初等数学知识，但是初等数学是高等数学的基础，而高等数学是初等数学的发展，高等数学对初等数学和中学数学具有一定的指导作用，为了解决学生从中学到大学这一突变所产生的诸多不适应问题，在中学教材和教学中适当地蕴含一些高等数学知识是必要的，事实上，中学教材和教辅读物中有不少地方都有一些高等数学知识的皱型和影子，这体现了我们教育家们的远见卓识，基于此，本文拟以柯西不等式为例，谈谈它在中学数学中的一些应用。 本文所说的柯西（Cauchy）不等式是指( i=1，2,……，n) （1）当且仅当时，等号成立。 这也是Holder不等式（其中k>1，k/>1，且，、，I=1，2，……，n）当k=2，k/=2时的情形。 不等式(1)的证明方法很多，中学生能接受的方法就有配方法、判别式法、数学归纳法等，这里不必赘述。 下面仅谈谈它在中学数学中的应用。 导出重要公式1、证明n个实数平方平均数不小于这n个数的算术平均数，即若，则 (2)证明：由柯西不等式所以故(2)式中当n=2时，为，这就是中学数学课本(下册)P15第11题。 不等式(2)把中学教材中仅有的“算术平均”，“几何平均”问题拓广到了“二次幂平均”问题，即，这不仅拓宽了中学生的眼界，而且为解决许多不等式的问题开辟了一条新路。 2、导出点到直线的距离公式，即点P(x0，y0)到直线l：Ax+By+C=0的距离上述非严格不等式仅在B(x1-x0)=A(y1-y0)，即PQ⊥l时取等号。 故公式，获证。 证明不等式利用柯西不等式证明某些不等式显得特别方便，在现行的高中教材中就有不少这样的题目，例如高中代数下册(必修)P32复习题五的第11题：已知，求证，此题的题设和题断一看就知道具有柯西不等式的开工，因而利用柯西不等式证明十分箪捷，(证略)。 又如P16第19题：已知a、b、c∈R+，求证，简证为：由柯西不等式，左边=。 获证。 下面再举一个含三角函数的不等式的证明题。 设a、b、c>0且acos2θ+bsin2θ
柯西不等式的简便证明方法？？
柯西不等式可以简单地记做：平方和的积 ≥ 积的和的平方。 它是对两列数不等式。 取等号的条件是两列数对应成比例。 如：两列数 0，1 和 2，3 有 (0^2 + 1^2) * (2^2 + 3^2) = 26 ≥ (0*2 + 1*3)^2 = 9. 形式比较简单的证明方法就是构造一个辅助函数，这个辅助函数是二次函数，于是用二次函数取值条件就得到Cauchy不等式。 还有一种形式比较麻烦的，但确实很容易想到的证法，就是完全把Cauchy不等式右边-左边的式子展开，化成一组平方和的形式。 我这里只给出前一种证法。 Cauchy不等式的形式化写法就是：记两列数分别是ai, bi，则有 (∑ai^2) * (∑bi^2) ≥ (∑ai * bi)^2. 我们令 f(x) = ∑(ai + x * bi)^2 = (∑bi^2) * x^2 + 2 * (∑ai * bi) * x + (∑ai^2) 则我们知道恒有 f(x) ≥ 0. 用二次函数无实根或只有一个实根的条件，就有 Δ = 4 * (∑ai * bi)^2 - 4 * (∑ai^2) * (∑bi^2) ≤ 0. 于是移项得到结论。 学了更多的数学以后就知道，这个不等式可以推广到一般的内积空间中，那时证明的书写会更简洁一些。 我们现在的证明只是其中的一个特例罢了。
